This function retrieves the latent factors and their variable loadings which
can be used as R objects to perform other analysis.
Arguments
- data
An
R objectobtained from exploratory factor analysis (EFA) using thefafunction inpsychpackage.- DATA
A
data.frame, the raw data used to carry out the parallel analysis to obtaindataobject.- RC
Optional factor indicating whether resilience capacity is to be estimated but defaults to
NULLonce the number of variables in the data is not sufficient, i.e. < 20. To estimate, turn it to "Yes".
Value
A list with the following components:
Loadings datadataframeof the factor loadings from the data.Factors extracteddataframeof retrieved latent factors.factored datadataframeof latent data based the product of recovered latent factors and the on raw data.Factors listA list of vectors of individual latent factors recovered from the data. However, to make it usable, the vector should be
bindwith the names of the variables in the data and theNAremoved.Resilence capacityA vector of the resilience capacity if the data is prepared for that otherwise NULL.
Examples
library(psych)
library(readr)
Data <- Quicksummary
GGn <- names(Data)
GG <- ncol(Data)
GGx <- c(paste0('x0', 1 : 9), paste("x", 10 : ncol(Data), sep = ""))
names(Data) <- GGx
lll <- fa.parallel(Data, fm = "minres", fa = "fa")
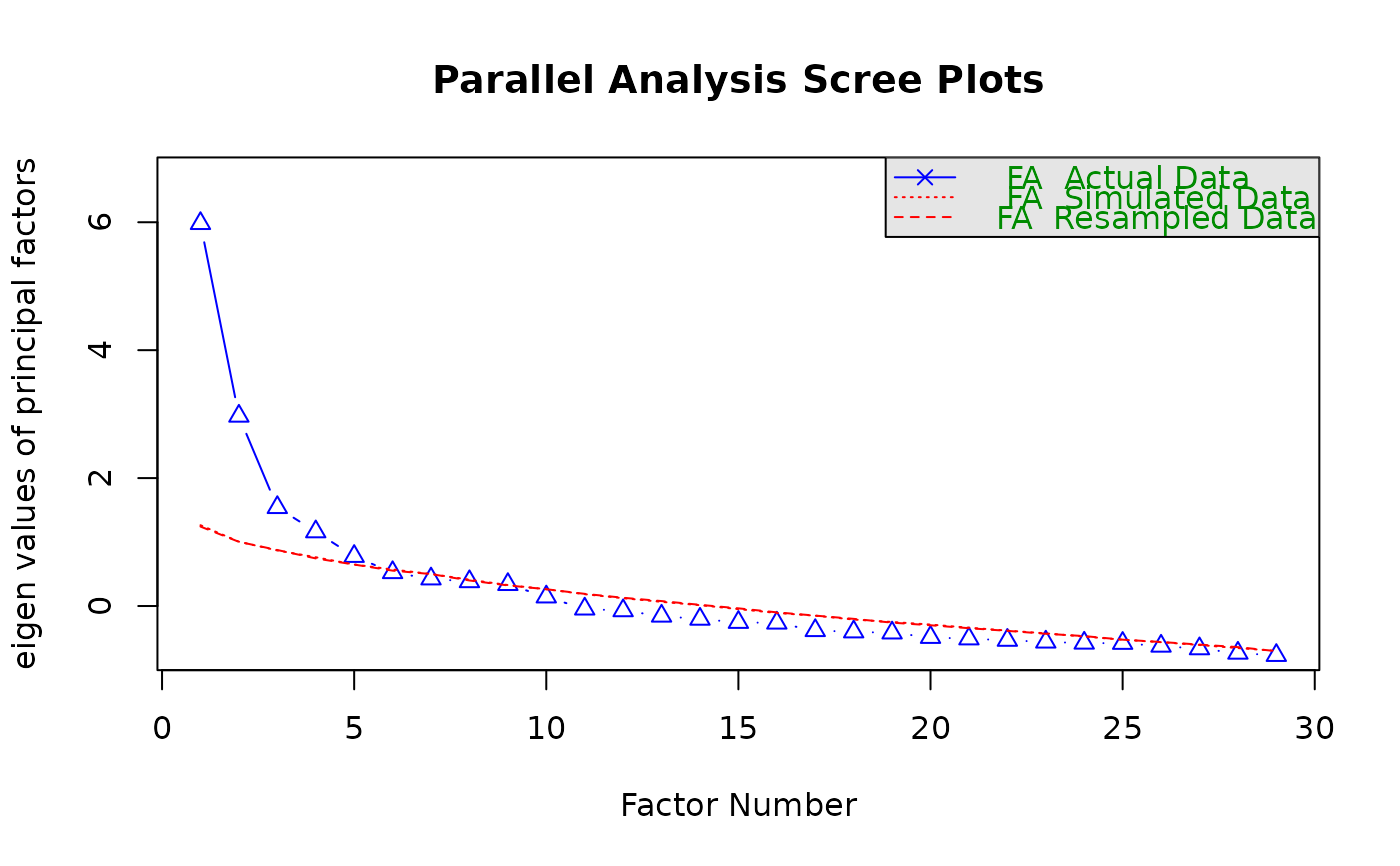#> Parallel analysis suggests that the number of factors = 5 and the number of components = NA
dat <- fa(Data, nfactors = lll[["nfact"]], rotate = "varimax",fm = "minres")
model_factors(data = dat, DATA = Data)
#>
#> Loadings:
#> MR1 MR2 MR3 MR5 MR4
#> x11 0.513 0.053 0.124 0.217 0.137
#> x12 0.611 0.127 -0.090 0.075 0.134
#> x13 0.559 0.354 0.115 0.020 -0.172
#> x20 0.556 0.049 0.083 0.306 0.059
#> x24 0.617 -0.284 -0.168 0.056 0.527
#> x25 0.718 -0.169 0.063 0.065 0.196
#> x26 0.595 0.048 0.104 0.205 0.139
#> x01 0.124 0.625 -0.077 -0.066 0.066
#> x02 0.039 0.783 -0.012 0.206 0.541
#> x10 0.254 0.631 -0.139 0.255 -0.081
#> x28 -0.086 -0.610 0.092 0.320 0.111
#> x04 0.239 -0.176 0.740 -0.101 -0.039
#> x05 0.149 0.065 0.792 0.074 -0.015
#> x06 -0.043 -0.260 0.720 0.157 0.186
#> x08 -0.130 0.016 0.594 0.255 0.452
#> x17 0.142 -0.192 0.044 0.667 0.137
#> x18 0.263 0.161 -0.041 0.527 0.073
#> x19 0.290 0.066 0.069 0.592 0.134
#> x03 0.087 -0.015 0.309 0.286 0.523
#> x07 0.302 -0.031 0.240 0.417 0.090
#> x09 0.112 -0.301 0.305 0.403 0.154
#> x14 0.345 0.153 0.203 0.203 -0.080
#> x15 0.480 0.275 0.262 0.069 -0.181
#> x16 0.125 -0.299 0.346 0.374 0.291
#> x21 0.492 -0.037 0.064 0.344 -0.065
#> x22 0.303 -0.238 0.039 0.286 0.481
#> x23 0.360 -0.440 0.021 0.207 0.499
#> x27 0.092 0.056 0.465
#> x29 0.216 -0.392 0.355 0.070 0.262
#>
#> MR1 MR2 MR3 MR5 MR4
#> SS loadings 3.854 2.895 2.786 2.441 2.203
#> Proportion Var 0.133 0.100 0.096 0.084 0.076
#> Cumulative Var 0.133 0.233 0.329 0.413 0.489
#> $`Loadings data`
#> Factor MR1 MR2 MR3 MR5 MR4
#> 1 1 0.513 0.053 0.124 0.217 0.137
#> 10 10 0.254 0.631 -0.139 0.255 -0.081
#> 11 11 -0.086 -0.610 0.092 0.320 0.111
#> 12 12 0.239 -0.176 0.740 -0.101 -0.039
#> 13 13 0.149 0.065 0.792 0.074 -0.015
#> 14 14 -0.043 -0.260 0.720 0.157 0.186
#> 15 15 -0.130 0.016 0.594 0.255 0.452
#> 16 16 0.142 -0.192 0.044 0.667 0.137
#> 17 17 0.263 0.161 -0.041 0.527 0.073
#> 18 18 0.290 0.066 0.069 0.592 0.134
#> 19 19 0.087 -0.015 0.309 0.286 0.523
#> 2 2 0.611 0.127 -0.090 0.075 0.134
#> 20 20 0.302 -0.031 0.240 0.417 0.090
#> 21 21 0.112 -0.301 0.305 0.403 0.154
#> 22 22 0.345 0.153 0.203 0.203 -0.080
#> 23 23 0.480 0.275 0.262 0.069 -0.181
#> 24 24 0.125 -0.299 0.346 0.374 0.291
#> 25 25 0.492 -0.037 0.064 0.344 -0.065
#> 26 26 0.303 -0.238 0.039 0.286 0.481
#> 27 27 0.360 -0.440 0.021 0.207 0.499
#> 28 28 0.000 0.092 0.056 0.000 0.465
#> 29 29 0.216 -0.392 0.355 0.070 0.262
#> 3 3 0.559 0.354 0.115 0.020 -0.172
#> 4 4 0.556 0.049 0.083 0.306 0.059
#> 5 5 0.617 -0.284 -0.168 0.056 0.527
#> 6 6 0.718 -0.169 0.063 0.065 0.196
#> 7 7 0.595 0.048 0.104 0.205 0.139
#> 8 8 0.124 0.625 -0.077 -0.066 0.066
#> 9 9 0.039 0.783 -0.012 0.206 0.541
#>
#> $`Factors extracted`
#> # A tibble: 29 × 6
#> Factor MR1 MR2 MR3 MR5 MR4
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 0.513 0 0 0 0
#> 2 10 0 0.631 0 0 0
#> 3 11 0 -0.61 0 0 0
#> 4 12 0 0 0.74 0 0
#> 5 13 0 0 0.792 0 0
#> 6 14 0 0 0.72 0 0
#> 7 15 0 0 0.594 0 0.452
#> 8 16 0 0 0 0.667 0
#> 9 17 0 0 0 0.527 0
#> 10 18 0 0 0 0.592 0
#> # ℹ 19 more rows
#>
#> $`factored data`
#> MR1 MR2 MR3 MR5 MR4
#> 1 19.292 -3.244 5.368 9.418 11.788
#> 2 17.852 -2.068 5.368 9.015 11.788
#> 3 17.804 1.711 5.368 6.892 11.788
#> 4 19.292 -3.244 5.368 9.418 11.788
#> 5 19.292 -3.244 5.368 8.826 11.788
#> 6 19.292 -3.244 5.368 9.418 11.788
#> 7 17.852 -3.244 4.628 7.434 12.253
#> 8 19.292 -3.244 5.368 8.826 11.788
#> 9 19.292 -3.244 5.368 8.826 11.788
#> 10 17.852 -3.244 4.628 7.434 12.253
#> 11 13.185 -2.083 4.180 6.183 7.375
#> 12 12.867 -1.643 3.440 8.781 4.948
#> 13 7.193 0.472 5.786 2.606 2.947
#> 14 11.210 -1.643 2.846 2.606 4.919
#> 15 9.629 -1.861 5.890 5.387 4.450
#> 16 20.614 -2.963 4.378 3.725 9.963
#> 17 11.499 -2.523 3.440 6.435 6.892
#> 18 5.141 -0.811 2.846 2.606 2.947
#> 19 7.193 -0.811 5.806 3.133 2.947
#> 20 12.590 -2.502 7.912 6.852 6.892
#> 21 20.885 0.470 14.230 10.550 14.933
#> 22 22.114 0.300 13.438 10.035 16.941
#> 23 19.346 1.503 14.230 10.086 14.520
#> 24 13.861 0.438 5.870 6.764 11.766
#> 25 16.868 1.476 3.586 8.162 11.684
#> 26 11.735 0.098 5.066 6.236 9.722
#> 27 20.465 2.733 10.018 7.812 10.087
#> 28 13.972 0.708 7.694 7.570 10.626
#> 29 22.698 0.300 12.916 11.559 14.497
#> 30 14.522 0.463 10.882 7.887 10.632
#> 31 23.309 0.252 12.124 12.613 15.519
#> 32 22.708 0.300 12.718 12.438 15.426
#> 33 16.808 -1.708 11.312 7.924 11.397
#> 34 15.782 -0.458 11.312 7.924 12.327
#> 35 16.808 -0.925 11.312 8.327 12.868
#> 36 15.782 -1.708 11.312 7.924 11.397
#> 37 15.782 -1.708 11.312 7.924 11.397
#> 38 16.338 -2.100 11.312 7.924 11.397
#> 39 13.827 -2.100 12.176 8.112 10.858
#> 40 16.454 -1.660 11.312 7.924 12.882
#> 41 15.782 -1.708 11.312 7.924 11.397
#> 42 15.782 -0.925 11.312 7.924 11.938
#> 43 11.057 -0.731 6.160 9.948 7.714
#> 44 11.057 -0.731 6.160 9.948 7.714
#> 45 12.518 -0.901 9.258 7.430 8.258
#> 46 12.271 0.053 5.870 9.004 6.416
#> 47 10.565 -0.949 4.920 8.724 6.852
#> 48 11.057 -0.731 6.160 9.948 7.714
#> 49 11.017 -0.339 7.620 8.711 8.121
#> 50 13.945 -0.827 8.340 8.522 6.746
#> 51 11.057 -0.731 6.160 9.142 7.714
#> 52 12.103 -3.355 8.664 8.174 8.756
#> 53 13.371 -2.502 7.172 7.475 7.822
#> 54 13.383 -1.182 9.694 8.406 10.162
#> 55 10.713 -1.182 9.100 7.475 7.694
#> 56 11.141 -2.502 8.716 9.031 9.333
#> 57 11.226 -1.182 7.172 5.894 6.790
#> 58 12.106 -2.502 8.412 9.031 9.191
#> 59 13.646 -2.502 9.476 9.031 9.814
#> 60 12.149 -3.286 8.412 9.031 8.726
#> 61 13.851 -2.502 13.636 8.439 11.199
#> 62 14.263 -3.678 11.978 9.031 12.659
#> 63 16.379 -2.439 9.476 8.471 8.319
#> 64 13.591 -2.089 14.230 9.808 11.833
#> 65 15.102 -3.292 14.230 10.642 11.709
#> 66 20.424 -1.781 8.538 10.475 9.803
#> 67 19.226 -1.580 9.998 8.536 8.358
#> 68 11.690 -3.414 10.664 6.925 10.243
#> 69 13.545 -0.811 4.628 5.568 9.722
#> 70 16.446 -1.431 13.636 8.504 10.347
#> 71 23.019 -3.663 9.944 11.836 14.283
#> 72 18.596 -1.171 8.902 7.857 10.126
#> 73 15.379 -2.238 7.224 8.211 8.858
#> 74 12.999 -2.238 7.224 8.211 8.858
#> 75 12.999 -2.238 7.224 8.211 8.858
#> 76 14.763 -3.414 8.810 6.449 8.937
#> 77 14.899 -1.628 5.838 6.449 10.456
#> 78 18.292 -1.829 10.050 10.841 10.348
#> 79 16.149 -1.781 9.258 7.527 7.857
#> 80 18.245 -2.412 7.944 9.480 9.862
#> 81 19.021 -2.852 7.818 9.897 10.348
#> 82 17.677 -2.242 10.090 10.410 10.348
#> 83 8.111 -0.557 6.734 11.179 4.450
#> 84 18.296 -1.393 7.600 8.967 12.269
#> 85 12.231 -2.068 11.384 6.605 8.419
#> 86 14.079 -4.055 9.132 8.770 10.722
#> 87 12.986 -1.989 6.466 6.686 5.320
#> 88 13.523 -1.798 10.498 8.223 5.777
#> 89 22.984 -4.686 8.110 8.554 11.965
#> 90 11.049 -3.060 10.270 12.503 6.965
#> 91 11.825 -2.083 11.998 7.448 8.837
#> 92 13.245 -1.622 10.342 7.363 4.919
#> 93 11.843 -2.364 10.196 5.879 6.421
#> 94 15.614 -1.733 8.320 7.327 8.774
#> 95 19.005 -3.286 8.464 7.605 11.788
#> 96 17.447 -2.364 5.692 6.988 5.894
#> 97 18.681 -1.580 5.692 6.988 6.948
#> 98 15.614 -1.733 8.320 7.327 8.774
#> 99 18.883 -1.733 5.692 6.018 7.870
#> 100 16.185 -2.364 5.692 7.605 5.894
#> 101 11.358 -2.295 5.672 8.851 4.345
#> 102 14.111 -3.244 5.692 6.396 5.900
#> 103 15.983 -2.364 5.692 6.018 6.483
#>
#> $`Factors list`
#> $`Factors list`$MR1
#> [1] 0.513 NA NA NA NA NA NA NA NA NA NA 0.611
#> [13] NA NA NA 0.480 NA 0.492 NA NA NA NA 0.559 0.556
#> [25] 0.617 0.718 0.595 NA NA
#>
#> $`Factors list`$MR2
#> [1] NA 0.631 NA NA NA NA NA NA NA NA NA NA
#> [13] NA NA NA NA NA NA NA NA NA NA NA NA
#> [25] NA NA NA 0.625 0.783
#>
#> $`Factors list`$MR3
#> [1] NA NA NA 0.740 0.792 0.720 0.594 NA NA NA NA NA
#> [13] NA NA NA NA NA NA NA NA NA NA NA NA
#> [25] NA NA NA NA NA
#>
#> $`Factors list`$MR5
#> [1] NA NA NA NA NA NA NA 0.667 0.527 0.592 NA NA
#> [13] 0.417 0.403 NA NA NA NA NA NA NA NA NA NA
#> [25] NA NA NA NA NA
#>
#> $`Factors list`$MR4
#> [1] NA NA NA NA NA NA 0.452 NA NA NA 0.523 NA
#> [13] NA NA NA NA NA NA 0.481 0.499 0.465 NA NA NA
#> [25] 0.527 NA NA NA 0.541
#>
#>
#> $`Resilence capacity`
#> NULL
#>